对于成功的数据分析而言,把握数据整体的性质是至关重要的,使用统计量来检查数据特征,主要是检查数据的集中程度、离散程度和分布形状,通过这些统计量可以识别数据集整体上的一些重要性质,对后续的数据分析,有很大的参考作用。
一,基本统计量
用于描述数据的基本统计量主要分为三类,分别是中心趋势统计量、散布程度统计量和分布形状统计量。
1,中心趋势统计量
中心趋势统计量是指表示位置的统计量,直观地说,给定一个属性,它的值大部分落在何处?
(1)均值
均值(mean)又称算数平均数,描述数据去指导额平均位置,数学表达式:均值 = ∑x / n;
有时,一组数据中的每个值可以和一个权重Wi相关联,权重反映的的是依附值的重要性或出现的频率,这种均值称作加权均值 = ∑xw / n;
尽管均值是描述数据集中心趋势的最有用的统计量,但是,它并非总是度量数据中心的最佳方法,这是因为,均值对极端值(离群点)很敏感。为了抵消少数极端值的影响,我们可以使用截尾均值,截尾均值是指丢弃极端值后的均值。
(2)中位数
对于倾斜(非对称)的数据,能够更好地描述数据中心的统计量是中位数(median),中位数是有序数据值的中间值,中位数可避免极端数据,代表这数据总体的中等情况。例如:从小到大排序,总数是奇数,取中间的数,总数是偶数,取中间两个数的平均数。
(3)众数
众数(mode)是变量中出现频率最大的值,通常用于对定性数据确定众数,例如:用户状态(正常,欠费停机,申请停机,拆机、消号),该变量的众数是“正常”,这种情况是正常的。
2,表示数据离散程度的统计量
度量数据离散程度的统计量主要是标准差和四分位极差。
(1)标准差(或方差)
标准差用于度量数据分布的离散程度,低标准差意味着数据观测趋向于靠近均值,高标准差表示数据散步在一个大的值域中。
(2)四分位极差
极差(range),也称作值域,是一组数据中的最大值和最小值的差, range = Max - Min。
百分位数(quantile)是把数据值按照从小到大的顺序排列,把数据分成100份。中位数是数据的中间位置上的数据,第一个四分位数记作Q1,是指第25个百分位上的数据,第三个四分位数记作(Q3),是指第75个百分位上的数据。
四分位极差(IQR)= Q3 - Q1 ,IQR是指第一个四分位和第三个四分位之间的距离,它给出被数据的中间一半所覆盖的范围,是表示数据离散程度的一个简单度量。
3,表示分布形状的统计量
分布形状使用偏度系数和峰度系数来度量,
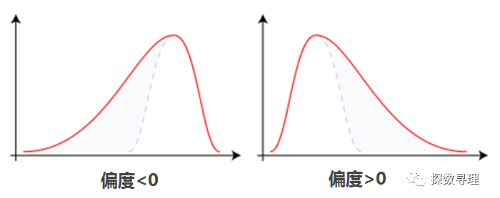
偏度是用于衡量数据分布对称性的统计量:通过对偏度系数的测量,我们能够判定数据分布的不对称程度以及方向。
- 对于正态分布(或严格对称分布)偏度等于0
- 若偏度为负, 则x均值左侧的离散度比右侧强;
- 若偏度为正, 则x均值左侧的离散度比右侧弱;
峰度是用于衡量数据分布陡峭或平滑的统计量,通过对峰度系数的测量,我们能够判定数据分布相对于正态分布而言是更陡峭还是平缓。
- 正态分布的峰度为3,
- 当时间序列的曲线峰值比正态分布的高时,峰度大于3;
- 当比正态分布的低时,峰度小于3。
(1)偏度系数
偏度系数反映数据分布偏移中心位置的程度,记为SK,则有 SK= (均值一中位数)/标准差。偏度系数是描述分布偏离对称性程度的一个特征数。
正态分布的偏度为0,偏度<0称分布具有负偏离(左偏态),此时数据位于均值左边的位于右边的多,有个尾巴拖到左边,说明左边有极端值,偏度>0称分布具有正偏离(右偏态)。偏度接近如于0 ,可认为分布对称。例如:知道分布有可能在偏度上偏离正态分布,则可用偏度来检验分布的正态性。偏度的绝对值数值越大表示其分布形态的偏斜程度越大。
(2)峰度系数
峰度系数(Kurtosis)用来度量数据在中心聚集程度,记为K,描述总体中所有取值分布形态陡缓程度的统计量(与正态分布比较,,就是正态分布的峰顶)。
例如:正态分布的峰度系数值是3,K>3的峰度系数说明观察量更集中,有比正态分布更短的尾部;K<3的峰度系数说明观测量不那么集中,有比正态分布更长的尾部。
峰度系数公式是:
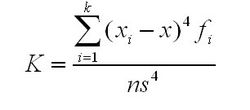
示例,本文使用vcd包中的Arthritis数据集来演示如何进行统计量分析:
head(Arthritis) ID Treatment Sex Age Improved57 Treated Male 27 Some46 Treated Male 29 None77 Treated Male 30 None17 Treated Male 32 Marked36 Treated Male 46 Marked23 Treated Male 58 Marked
其中变量Improved和Sex是因子类型,ID和Age是数值类型。
二,集中趋势度量
集中趋势通过均值、中位数和众数来度量。
1,均值
均值是所有数据的平均值,使用mean()函数来计算向量的均值:
age.mean <- mean(Arthritis$Age)
有时,为了反映在均值中不同成分所占的权重,为数据中的每个元素Xi 赋予一个权重Wi,这样就得到了加权平均值,使用weighted.mean(x,w)来计算加权平均值。
weighted.mean(x,w)
x为数据向量,w为权重向量,x中每一个元素都对应w中的一个权重值。
根据Sex来设置权重(weight),男性的Age的权重为95%,女性的Age的权重为105%,那么得到的加权平均值是:
age.wt <- ifelse(Arthritis$Sex=="Male",0.95,1.05)age.wt.mean <- weighted.mean(Arthritis$Age,age.wt)
如果数据中存在极端值或者数据是偏态分布的,那么均值就不能很好地度量数据的集中趋势,为了消除少数极端值的影响,可以使用截断均值或者中位数来度量数据的集中趋势。截断均值是指去掉极端值之后的平均值。
2,中位数
中位数是把一组观察值从小到大按顺序排列,位于中间的那个数据。使用median(x)计算中位数。
age.median <- median(Arthritis$Age)
3,众数
众数是指数据集中出现最频繁的值,众数常用于定性数据。R没有标准的内置函数来计算众数,因此,我们将创建一个用户自定义函数来计算数据集的众数。
该函数以向量作为输入,以众数值作为输出。
getmode <- function(v) { uniqv <- unique(v) uniqv[which.max(tabulate(match(v, uniqv)))]} 三,离中趋势度量
衡量离中趋势的四个度量值:
- 值域(Range)的计算公式:Range = Max - Min
- 标准差:度量数据偏离均值的程度
- 变异系数(CV):变异系数度量标准差相对于均值的离中趋势,计算公式是:CV=标准差/均值
- 四分位数间距(IQR)是上四分位数QU和下四分位数QL之差,其间包含全部观察值的一般,其值越大,说明数据的变异程度越大,离中趋势越明显。
查看Arthritis数据集的离中趋势:
get_stat <- function(v){ v.mean <- mean(v) v.median <- median(v) v.range <- max(v)-min(v) v.sd <- sd(v) v.cv <- v.sd/v.mean v.iqr <- quantile(v,0.75) - quantile(v,0.25) d.stat <- data.frame(mean=v.mean,median=v.median,range=v.range,sd=v.sd,cv=v.cv,iqr=v.iqr, row.names = NULL) } mystat <- get_stat(Arthritis$Age) 四,偏度和峰度
基础安装包中没有提供计算偏度和峰度的函数,用户可以自行添加:
mystats <- function(x, na.omit=FALSE){ if (na.omit) x <- x[!is.na(x)] m <- mean(x) n <- length(x) s <- sd(x) skew <- sum((x-m)^3/s^3)/n kurt <- sum((x-m)^4/s^4)/n - 3 return(c(n=n, mean=m, stdev=s, skew=skew, kurtosis=kurt))}myvars <- c("mpg", "hp", "wt")sapply(mtcars[myvars], mystats) 为大家推荐一篇文章:,引用该文中的峰度影响实验的结论:
尾部或离群点对峰度影响为正向,且影响程度最大。而高概率区对峰度影响也为正向,但是比较少;而山腰位置,中等概率区域则影响为负向。
参考文档: